目录
- 1 查找基本概念
- 2 线性表的查找
- 2.1 顺序查找
- 2.2 二分法查找
- 2.3 分块查找
- 3 树表的查询
- 3.1 二叉排序树
- 3.1.1 定义
- 3.1.2 二叉树的建立、遍历、查找、增加、删除:
- 3.1.3 代码实现:
- 3.2 平衡二叉树
- 3.2.1 平横因子
- 3.2.2 不平横树的调整-左旋
- 3.2.3 不平横树的调整-右旋
- 3.2.4 当插入节点出现失衡因子如何旋转
- 3.2.4 某位UP主的详细视频讲解
- 3.3 B-树
- 3.3.1 B-树的定义
- 3.3.2 题目练习
- 3.3.3 B-树的查找、插入、删除
- 3.4 B+树
- 4 散列表查找(哈希表查找)
- 4.1 基本术语和概念
- 4.2 散列函数的构造
- 4.3 哈希表的创建,插入,查找
- 4.3.1 程序实现
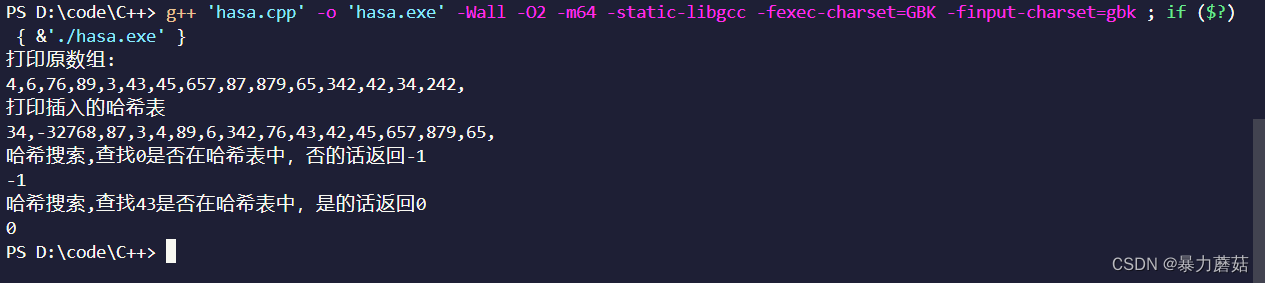
- 4.3.2 程序结果:
常用的查找及代码程序
1 查找基本概念
查找是在数据集合中寻找特定元素或满足特定条件的元素的过程。它是一种常见的数据操作。
2 线性表的查找
2.1 顺序查找
顺序查找(Sequential Search)的查找过程为:从表的一端开始,依次将记录的关键字和给定值进行比较,若某个记录的关键字和给定值相等,则查找成功;反之,若扫描整个表后,仍未找到关键字和给定值相等的记录,则查找失败。
顺序查找方法既适用于线性表的顺序存储结构,又适用千线性表的链式存储结构。下面只介绍以顺序表作为存储结构时实现的顺序查找算法。顺序查找比较简单,但是费时;效率低;
简单看一下下面两个算法的区别:arr【0】不用于存储数据;
// 顺序查找函数
int search(int arr[], int size, int key) {
// 从数组的最后一个元素开始查找
for (int i = size - 1; i >= 1; --i) {
if (arr[i] == key) {
return i;
}
}
// 未找到元素
return 0;
}
改进后:不用每次都进行循环是否结束的查找,也就是i>=1?
// 顺序查找函数
int search(int arr[], int size, int key) {
// 设置监视哨
arr[0] = key;
// 从数组的最后一个元素开始查找
for (int i = size; arr[i]!=key; --i);
// 未找到元素
return i;
}
2.2 二分法查找
它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构, 而且表中元素按关键字有序排列;
例如查找30的数据:( 5, 16, 20, 27, 3 0, 36, 44, 55, 60, 67, 71)
思考如果low=mid而不是low=mid+1后结果是什么?
需要注意的是,循环执行的条件是low< =high,而不是low<high,因为low=high时,查找区间还有最后一个结点, 还要进一步比较 。
// 二分法查找函数
int main()
{
int high, mid, low, t;
int str[] = {5, 16, 20, 27, 30, 36, 44, 55, 60, 67, 71};
high = 10;
low = 0;
mid = (high + low) / 2;
t = 71;
while (low <= high){
mid = (high + low) / 2;
if (str[mid] >= t){
if (str[mid] == t){
printf("YES\n");
return 0;
}
else{
high = mid;
}
}
else{
low = mid + 1; // 思考如果low=mid后结果是什么?如果
// t=71,会在后面陷入死循环:high=10,low=9,mid=9;一直循环
}
}
return 0;
}
折半查找的优点是:比较次数少,查找效率高。其缺点是:对表结构要求高,只能用于顺序存储的有序表。查找前需要排序,而排序本身是一种费时的运算。同时为了保持顺序表的有序性,对有序表进行插入和删除时,平均比较和移动表中一半元素,这也是一种费时的运算。因此,折半查找不适用于数据元素经常变动的线性表。
2.3 分块查找
分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。 由于块内是无序的,故插入和删除比较容易,无需进行大量移动。 如果线性表既要快速查找又经常动态变化,则可采用分块查找。
其缺点是:要增加一个索引表的存
储空间并对初始索引表进行排序运算。
其基本的思想和这里面差不多;如下图:

3 树表的查询
前面介绍的3 种查找方法都是用线性表作为查找表的组织形式,其中折半查找效率较高。但由千折半查找要求表中记录按关键字有序排列,且不能用链表做存储结构,因此,当表的插入或删除操作频繁时,为维护表的有序性,需要移动表中很多记录。这种由移动记录引起的额外时间开销,就会抵消折半查找的优点。 所以,线性表的查找更适用千静态查找表,若要对动态查找表进行高效率的查找,可采用几种特殊的二叉树作为查找表的组织形式,在此将它们统称为树表。 本节将介绍在这些树表上进行查找和修改操作的方法
3.1 二叉排序树
3.1.1 定义
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:二叉排序树,又称二叉查找树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若右子树不空,则右子树上所有节点的值均大于它的根节点的值;
左、右子树也分别为二叉排序树。
如下图所示:

若中序遍历图7.5(a), 则可得到一个按数值 大小排序的递增序列:
3, 12, 24, 37, 45, 53, 61, 78, 90, 100
3.1.2 二叉树的建立、遍历、查找、增加、删除:
若中序遍历图7.5(a), 则可得到一个按数值 大小排序的递增序列:具体详情可以参考我下面的这篇内容:主要是包括二叉排序树(建立、遍历、查找、增加、删除)并给出了详细的C运行代码;链接:
3.1.3 代码实现:
二叉排序树(建立、遍历、查找、增加、删除)并给出了详细的C运行代码;链接
3.2 平衡二叉树
二叉排序树查找算法的性能取决于二叉树的结构,而 二叉排序树的形状则取决于其数据集。如果数据呈有序排列,则二叉排序树是线性的,查找的时间复杂度为O(n); 反之,如果二叉排序树的结构合理,则查找速度较快,查找的时间复杂度为 O(lo2n)。事实上,树的高度越小,查找 g速度越快。因此,希望二叉树的高度尽可能小。本节将讨论一种特殊类型的二叉排序树,称为平衡二叉树 (Balance d Binary Tree或Height-Balanced·Tree), 因由前苏联数学家Adelson-Velskii和Land i s提出,所以又称AVL树。
平衡二叉树或者是空树,或者是具有如下特征的二叉排序树:
- (1 )
左子树和右子树的深度之差的绝对值不超过1; - (2)
左子树和右子树也是平衡二叉树。
3.2.1 平横因子
平衡因子=左子树高度-右子树高度:如下图所示:


3.2.2 不平横树的调整-左旋
在旋转过程中,冲突的是9的左孩6,这里记一句话左旋--冲突左孩变右孩;如下图左旋过程

而且旋转过后,中序遍历的话,两者是等价的,但是树的高度却变低了;如下图:

3.2.3 不平横树的调整-右旋
在旋转过程中,冲突的是14的左孩9,这里记一句话右旋--冲突右孩变左孩;如下图左旋过程

而且旋转过后,中序遍历的话,两者是等价的,但是树的高度却变低了;如下图:

3.2.4 当插入节点出现失衡因子如何旋转
调整方法是:找到离插入结点最近且平衡因子绝对值超过1的祖先结点, 以该结点为根的子树称为最小不平衡子树, 可将重新平衡的范围局限于这棵子树,如下图所示,一共四种情况:
巧记一下:LL是右旋,RR是左旋,也就是纯的则相反旋转:L(left),R(right)
巧记一下:LR是右旋,先左后右,RL,先右后左,也就是混的按照字母:L(left),R(right)

3.2.4 某位UP主的详细视频讲解
关于平衡二叉树的详细信息,这个视频讲的异常清晰:链接
3.3 B-树
前面介绍的查找方法均适用千存储在计算机内存中较小的文件,统称为内查找法。若文件很大且存放于外存进行查找时,这些查找方法就不适用了。内查找法都以结点为单位进行查找,这样需要反复地进行内、外存的交换,是很费时的。1970年,R.Bayer和£.Mccreight提出了一种适用于外查找的平衡多叉树-B-树,磁盘管理系统中的目录管理,以及数据库系统中的索引组织多数都采用B-树这种数据结构。
B树就是一个有序的多路查询树
3.3.1 B-树的定义
- 对于m叉树,每个节点最多有m个孩子,其中最多有m-1个关键字;(人5个手指最多4条缝)
- 每个节点的内容如下:例如对于四叉树,3个关键字,即其存储结构:
| n:多少关键字 | P0指针 | k1关键字 | P1指针 | k2关键字 | P2指针 | k3关键字 | P3指针 |
|---|
- 每个节点的内容如下:例如对于四叉树,3个关键字,即其存储结构:
谨记m阶子树,最多有m-1个关键字,而对于每个节点最少要有[m/2]-1个关键字,其中[m/2]是向上取整;关键字就是把内容进行了分块,如同索引,例如:2--- 5,两个关键字就分量三个区域,0-2,2-5,5--三个范围,也就是对于四叉树,最多是3个关键字;
3.3.2 题目练习
真题练习:


3.3.3 B-树的查找、插入、删除
代码实现——C:链接
/*
* @Author: Xyh4ng
* @Date: 2023-01-02 20:24:30
* @LastEditors: Xyh4ng
* @LastEditTime: 2023-01-05 20:17:06
* @Description:
* Copyright (c) 2023 by Xyh4ng 503177404@qq.com, All Rights Reserved.
*/
#include <stdio.h>
#include <stdlib.h>
#define M 3 // B树的阶
#define MIN_KEYNUM (M + 1) / 2 - 1
typedef struct BTreeNode
{
int keyNum; // 结点中关键字的数量
struct BTreeNode *parent; // 指向双亲结点
struct Node // 存放关键字以及其孩子节点指针,正常结点最多存放m个孩子,但在插入判断时会多存放一个
{
int key;
struct BTreeNode *ptr;
} node[M + 1]; // key的0号单元未使用
} BTreeNode, *BTree;
typedef struct Result
{
int tag; // 查找成功的标志
BTreeNode *pt; // 指向查找到的结点
int i; // 结点在关键字中的序号
} Result;
int Search(BTree T, int K)
{
int i = 0;
for (int j = 1; j <= T->keyNum; j++)
{
if (T->node[j].key <= K)
{
i = j;
}
}
return i;
}
/* 在m阶B树T上查找关键字K,返回结果(pt,i,tag)。若查找成功,则特征值tag=1,指针pt所指结点中第i个关键字等于K;否则特征值tag=0,等于K的关键字应插入在指针Pt所指结点中第i和第i+1个关键字之间。 */
Result SearchBTree(BTree T, int K)
{
BTree p = T, q = NULL; /* 初始化,p指向待查结点,q指向p的双亲 */
int found = 0;
int index = 0;
Result r;
while (p && !found)
{
index = Search(p, K); // p->node[index].key ≤ K < p->node[index+1].key
if (index > 0 && p->node[index].key == K)
found = 1;
else
{
q = p;
p = p->node[index].ptr;
}
}
r.i = index;
if (found) // 查找成功
{
r.tag = 1;
r.pt = p;
}
else
{
r.tag = 0;
r.pt = q;
}
return r;
}
void Insert(BTree *q, int key, BTree ap, int i)
{
for (int j = (*q)->keyNum; j > i; j--) // 空出(*q)->node[i+1]
{
(*q)->node[j + 1] = (*q)->node[j];
}
(*q)->node[i + 1].key = key;
(*q)->node[i + 1].ptr = ap;
(*q)->keyNum++;
}
// 将结点q分裂成两个结点,mid之前的结点保留,mid之后结点移入新生结点ap
void Split(BTree *q, BTree *ap)
{
int mid = (M + 1) / 2;
*ap = (BTree)malloc(sizeof(BTreeNode));
(*ap)->node[0].ptr = (*q)->node[mid].ptr;
if ((*ap)->node[0].ptr)
{
(*ap)->node[0].ptr->parent = *ap;
}
for (int i = mid + 1; i <= M; i++)
{
(*ap)->node[i - mid] = (*q)->node[i];
if ((*ap)->node[i - mid].ptr)
{
(*ap)->node[i - mid].ptr->parent = *ap;
}
}
(*ap)->keyNum = M - mid;
(*ap)->parent = (*q)->parent;
(*q)->keyNum = mid - 1;
}
// 生成含信息(T,r,ap)的新的根结点&T,原T和ap为子树指针
void NewRoot(BTree *T, int key, BTree ap)
{
BTree p;
p = (BTree)malloc(sizeof(BTreeNode));
p->node[0].ptr = *T; // 根结点孩子数最小为2,则将T作为左孩子,ap作为右孩子
*T = p;
if ((*T)->node[0].ptr)
{
(*T)->node[0].ptr->parent = *T;
}
(*T)->parent = NULL;
(*T)->keyNum = 1;
(*T)->node[1].key = key;
(*T)->node[1].ptr = ap;
if ((*T)->node[1].ptr)
{
(*T)->node[1].ptr->parent = *T;
}
}
/* 在m阶B树T上结点*q的key[i]与key[i+1]之间插入关键字K的指针r。若引起结点过大,则沿双亲链进行必要的结点分裂调整,使T仍是m阶B树。 */
void InseartBTree(BTree *T, int key, BTree q, int i)
{
BTree ap = NULL;
int finished = 0;
int rx = key; // 需要插入的关键字的值
int mid;
while (q && !finished)
{
Insert(&q, rx, ap, i);
if (q->keyNum < M)
finished = 1;
else // 结点关键字数超出规定
{
int mid = (M + 1) / 2; // 结点的中间关键字序号
rx = q->node[mid].key;
Split(&q, &ap); // 将q->key[mid+1..M],q->ptr[mid..M]移入新结点*ap
q = q->parent;
if (q)
i = Search(q, rx);
}
}
if (!finished)
{
NewRoot(T, rx, ap);
}
}
void Delete(BTree *q, int index)
{
for (int i = index; i <= (*q)->keyNum; i++)
{
(*q)->node[index] = (*q)->node[index + 1];
}
(*q)->keyNum--;
}
void LeftRotation(BTree *q, BTree *p, int i)
{
// 将父亲结点转移至q结点的末尾
(*q)->keyNum++;
(*q)->node[(*q)->keyNum].key = (*p)->node[i + 1].key;
// 将q结点的右兄弟的第一个关键字转移至父亲结点的分隔符位置
BTree rightBroPtr = (*p)->node[i + 1].ptr;
(*p)->node[i + 1].key = rightBroPtr->node[1].key;
// 将右结点的关键字前移
for (int j = 1; j < rightBroPtr->keyNum; j++)
{
rightBroPtr->node[j] = rightBroPtr->node[j + 1];
}
rightBroPtr->keyNum--;
}
void RightRotation(BTree *q, BTree *p, int i)
{
// 将q结点向后移动空出第一个关键字的位置
for (int j = (*q)->keyNum; j >= 1; j--)
{
(*q)->node[j + 1] = (*q)->node[j];
}
// 将父亲结点移动至q结点的第一个关键字的位置
(*q)->node[1].key = (*p)->node[i].key;
(*q)->node[1].ptr = NULL;
(*q)->keyNum++;
// 将左兄弟结点的最后一个关键字移动至父亲结点的分隔符位置
BTree leftBroPtr = (*p)->node[i - 1].ptr;
(*p)->node[i].key = leftBroPtr->node[leftBroPtr->keyNum].key;
leftBroPtr->keyNum--;
}
void BalanceCheck(BTree *q, int key);
void MergeNode(BTree *q, BTree *p, int i)
{
BTree rightBroPtr = NULL, leftBroPtr = NULL;
if (i + 1 <= (*p)->keyNum)
{
rightBroPtr = (*p)->node[i + 1].ptr;
}
if (i - 1 >= 0)
{
leftBroPtr = (*p)->node[i - 1].ptr;
}
if (rightBroPtr)
{
// 将父亲结点的分隔符移动至q结点的最后
(*q)->keyNum++;
(*q)->node[(*q)->keyNum].key = (*p)->node[i + 1].key;
// 将右兄弟结点都移动到q结点上
(*q)->node[(*q)->keyNum].ptr = rightBroPtr->node[0].ptr;
for (int j = 1; j <= rightBroPtr->keyNum; j++)
{
(*q)->keyNum++;
(*q)->node[(*q)->keyNum] = rightBroPtr->node[j];
}
// 将父亲结点的分隔符删除
int key = (*p)->node[i + 1].key;
for (int j = i + 1; j < (*p)->keyNum; j++)
{
(*p)->node[j] = (*p)->node[j + 1];
}
(*p)->keyNum--;
if (!(*p)->parent && !(*p)->keyNum)
{
// 判断父亲结点是否为根结点,且关键字为空
// 让q结点作为根结点
(*q)->parent = NULL;
(*p) = (*q);
}
BalanceCheck(p, key);
}
else if (leftBroPtr)
{
// 将父亲结点的分隔符移动至左兄弟结点的最后
leftBroPtr->keyNum++;
leftBroPtr->node[leftBroPtr->keyNum].key = (*p)->node[i].key;
// 将q结点都移动到左兄弟结点上
leftBroPtr->node[leftBroPtr->keyNum].ptr = (*q)->node[0].ptr;
for (int j = 1; j <= (*q)->keyNum; j++)
{
leftBroPtr->keyNum++;
leftBroPtr->node[leftBroPtr->keyNum] = (*q)->node[j];
}
// 将父亲结点的分隔符删除
int key = (*p)->node[i].key;
for (int j = i; j < (*p)->keyNum; j++)
{
(*p)->node[j] = (*p)->node[j + 1];
}
(*p)->keyNum--;
if (!(*p)->parent && !(*p)->keyNum)
{
// 判断父亲结点是否为根结点,且关键字为空
// 让q结点作为根结点
(*q)->parent = NULL;
(*p) = (*q);
}
BalanceCheck(p, key);
}
}
void BalanceCheck(BTree *q, int key)
{
if ((*q)->keyNum < MIN_KEYNUM) // 该结点不满足最小关键字数目要求
{
BTree p = (*q)->parent;
int i = Search(p, key); // 找到q结点在父亲结点中的索引
if (i + 1 <= p->keyNum && p->node[i + 1].ptr->keyNum > MIN_KEYNUM) // 看q结点的右兄弟是否存在多余结点
{
LeftRotation(q, &p, i);
}
else if (i - 1 >= 0 && p->node[i - 1].ptr->keyNum > MIN_KEYNUM) // 看q结点的左兄弟是否存在多余结点
{
RightRotation(q, &p, i);
}
else // q结点的左右兄弟都不存在多余结点
{
// 将q结点和其左右兄弟的其中一个以及父亲结点中的分隔符合并
MergeNode(q, &p, i);
}
}
}
void MergeBro(BTree *left, BTree *right)
{
if (!(*left)->node[((*left)->keyNum)].ptr)
{
// 如果左子树为叶子结点
(*left)->node[(*left)->keyNum].ptr = (*right)->node[0].ptr;
for (int j = 1; j <= (*right)->keyNum; j++)
{
(*left)->keyNum++;
(*left)->node[(*left)->keyNum] = (*right)->node[j];
}
}
else
{
// 左子树不是叶子结点,则先将左子树最后一个子结点和右子树第一个子结点合并
MergeBro(&(*left)->node[(*left)->keyNum].ptr, &(*right)->node[0].ptr);
for (int j = 1; j <= (*right)->keyNum; j++)
{
(*left)->keyNum++;
(*left)->node[(*left)->keyNum] = (*right)->node[j];
}
}
// 合并完对左子树关键字数目进行判断
if ((*left)->keyNum >= M)
{
int mid = (M + 1) / 2; // 结点的中间关键字序号
int rx = (*left)->node[mid].key;
BTree ap = NULL;
Split(&(*left), &ap); // 将q->key[mid+1..M],q->ptr[mid..M]移入新结点*ap
BTree p = (*left)->parent;
int i = Search(p, rx);
Insert(&p, rx, ap, i);
}
}
void DeleteBTreeNode(BTree *T, int key)
{
Result res = SearchBTree(*T, key);
if (res.tag) // 查找成功
{
// 判断该结点是否是叶子结点
if (!res.pt->node[res.i].ptr)
{
// 若是叶子结点,则直接删除,然后对该结点进行平衡判断
Delete(&res.pt, res.i);
BalanceCheck(&res.pt, key);
}
else
{
// 若不是叶子节点
BTree leftChildPtr = res.pt->node[res.i - 1].ptr;
BTree rightChildPtr = res.pt->node[res.i].ptr;
if (leftChildPtr->keyNum > MIN_KEYNUM) // 左子树富有,则将左子树中提取最大值放到该结点中替换要删除的关键字
{
res.pt->node[res.i].key = leftChildPtr->node[leftChildPtr->keyNum].key;
leftChildPtr->keyNum--;
}
else if (rightChildPtr->keyNum > MIN_KEYNUM) // 右子树富有,则将右子树中提取最小值放到该结点中替换要删除的关键字
{
res.pt->node[res.i].key = rightChildPtr->node[1].key;
for (int j = 1; j < rightChildPtr->keyNum; j++)
{
rightChildPtr->node[j] = rightChildPtr->node[j + 1];
}
rightChildPtr->keyNum--;
}
else // 左右子树都不富有,则合并左右子树
{
MergeBro(&leftChildPtr, &rightChildPtr);
// 删除结点的关键字
res.i = Search(res.pt, key); // 合并结点可能会改变结点中关键字的次序,重新查序
for (int j = res.i; j < res.pt->keyNum; j++)
{
res.pt->node[j] = res.pt->node[j + 1];
}
res.pt->keyNum--;
// 对结点进行平衡判断
BalanceCheck(&res.pt, key);
}
}
}
else // 查找失败
{
printf("您删除的元素不存在");
}
}
int main()
{
int r[16] = {22, 16, 41, 58, 8, 11, 12, 16, 17, 9, 23, 13, 52, 58, 59, 61};
BTree T = NULL;
Result s;
int i;
for (int i = 0; i < 16; i++)
{
s = SearchBTree(T, r[i]);
if (!s.tag)
InseartBTree(&T, r[i], s.pt, s.i);
}
while (1)
{
printf("\n请输入要删除的关键字: ");
scanf("%d", &i);
DeleteBTreeNode(&T, i);
}
}
3.4 B+树
B+ 树是一种 B-树的变形树,更适合用于文件索引系统。严格来讲,它已不符合第 5 章中定
义的树了。这里仅进行概念的了解,详细信息可后序用到在进行熟悉。
4 散列表查找(哈希表查找)
前面讨论了基于线性表、树表结构的查找方法,这类查找方法都是以关键字的比较为基础的。散
列查找法(哈希查找) 的思想,它通过对元素的关键字值进行某种运算,直接求出元素的地址, 即使用关键字到地址的直接转换方法,而不需要反复比较。因此,散列查找法又叫杂凑法或散列法。
4.1 基本术语和概念
- 散列函数和地址:用于计算数据元素的哈希值。在记录的存储位置p和其关键字key 之间建立一个确定的对应关系H, 使 p=H( key ), 称这个对应关系H为散列函数,p为散列地址
- 散列表:存储数据元素的结构。一个有限连续的地址空间,用以存储按散列函数计算得到相应散列地址的数据记录。通常散列表的存储空间是一个一维数组,散列地址是数组的下标。
- 冲突和同义词:不同数据元素计算出的哈希值相同的情况。,那么这相同的哈希值就是同义词;
- 解决冲突的方法:如开放定址法、链地址法等。
4.2 散列函数的构造
常用的方法分类:
- 数字分析法
- 平方取中法
- 折叠法
- 除留余数法,如下图:

4.3 哈希表的创建,插入,查找
4.3.1 程序实现
这里哈希函数采用除留余数法,解决冲突的方法采用开放定址线性探测法.
这里如果中文输出乱码可以参考下列文章. 链接:
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define HASIZE 17
// 哈希表进行初始化时要保证其初始值不为要查询的值,
// 下面的值就是进行初始化的表值,一般不会重复
#define NULLKEY -32768
typedef struct hashtable
{
int *key;
int count; // 当前元素的个数
} HashTable;
// 哈希表的初始化
int InitHashtable(HashTable *H)
{
H->count = HASIZE;
H->key = (int *)malloc(sizeof(int) * HASIZE);
if (!H->key)
{
return -1; // 空间分配失败
}
// 初始化
for (int i = 0; i < HASIZE; i++)
{
(H->key)[i] = NULLKEY;
}
return 0; // 返回0代表初始化成功
}
// 使用除余留数法
int Hash(int key)
{
return key % HASIZE;
}
// 插入函数
void HashInsert(HashTable *H, int key)
{
// 先定义一个地址
int addr;
addr = Hash(key);
// 第一种情况就是一次插入就完成,也就是o(1)
// 第二种情况就是有了冲突,也就是第一次取的
// 模不为初始值,这时候就要进行,开放地址线性探测法
// 这两种相同点就是最后都要把key值插入表中,因此可以稍微合并一下,对下面的代码进行改进
// if ((H->key)[addr] == NULLKEY)
// {
// (H->key)[addr] = key;
// }
// else
// {
// while ((H->key)[addr] != NULLKEY)
// {
// // addr = Hash(addr+1);//或者
// addr = (addr + 1) % HASIZE;
// }
// // 循环结束的条件是找到了空位,进行插入
// (H->key)[addr] = key;
// }
// 改进代码情况
while ((H->key)[addr] != NULLKEY)
{
// addr = Hash(addr+1);//或者
addr = (addr + 1) % HASIZE;
}
// 循环结束的条件是找到了空位,进行插入
(H->key)[addr] = key;
}
// 搜索函数,传入一个地址,如果找到的话就让这个地址指向数据
int HashSerach(HashTable H, int key, int *addr)
{
*addr = Hash(key);
while (H.key[*addr] != key)
{
// 有两种情况是没有找到
// 第一就是遇到了NULLKEY,第二种就是循环到了自己本身
*addr = (*addr + 1) % HASIZE;
if (H.key[*addr] == NULLKEY || H.key[*addr] == key)
{
// 返回-1代表查询失败
return -1;
}
}
// 返回0代表查询成功,并且addr指针指向目标数据
return 0;
}
int main()
{
int arr[15] = {4, 6, 76, 89, 3, 43, 45, 657, 87, 879, 65, 342, 42, 34, 242};
HashTable H;
int *adrr = NULL;
int j;
int i;
adrr = &j;
InitHashtable(&H);
printf("打印原数组:\n");
for (int i = 0; i < 15; i++)
{
printf("%d,", arr[i]);
HashInsert(&H, arr[i]);
} // 插入完毕
// 打印出来:
printf("\n打印插入的哈希表\n");
for (int i = 0; i < 15; i++)
{
printf("%d,", H.key[i]);
} // 插入完毕
// 哈希搜索,查找0是否在哈希表中,否的话返回-1
printf("\n哈希搜索,查找0是否在哈希表中,否的话返回-1");
i = HashSerach(H, 0, adrr);
printf("\n%d", i);
printf("\n哈希搜索,查找43是否在哈希表中,是的话返回0");
i = HashSerach(H, 43, adrr);
printf("\n%d", i);
return 0;
}
4.3.2 程序结果: